Typesetting the CKM unitarity relations
You wouldn't think that typesetting the Cabibbo-Kobayashi-Maskawa (CKM) matrix's unitarity and normalisation relations would be hard, would you? Well, depending on how anal retentive you are it's either just a case of whacking in the right subscript indices or it's a minor voyage of discovery into how LaTeX doesn't always know best. When it comes to math typesetting I'm quite picky, so you can safely assume that I consider this to be a nice example of the latter!
A first try
First, lets try it the naive way. Put this in your LaTeX source, using
\usepackage{amsmath} in the document preamble:
\begin{subequations} \label{eq:CKMUnitarityRelations} \begin{equation} V_{ud}V_{ub}^{*} + V_{cd}V_{cb}^{*} + V_{td}V_{tb}^{*} &= 0 \qquad (db) \label{eq:CKMRelnDB} \\ V_{us}V_{ub}^{*} + V_{cs}V_{cb}^{*} + V_{ts}V_{tb}^{*} &= 0 \qquad (ds) \label{eq:CKMRelnDS} \\ V_{ud}V_{us}^{*} + V_{cd}V_{cs}^{*} + V_{td}V_{ts}^{*} &= 0 \qquad (sb) \label{eq:CKMRelnSB} \end{equation} \begin{equation} V_{ud}V_{td}^{*} + V_{us}V_{ts}^{*} + V_{ub}V_{tb}^{*} &= 0 \qquad (ut) \label{eq:CKMRelnUT} \\ V_{cd}V_{td}^{*} + V_{cs}V_{ts}^{*} + V_{cb}V_{tb}^{*} &= 0 \qquad (ct) \label{eq:CKMRelnCT} \\ V_{ud}V_{cd}^{*} + V_{us}V_{cs}^{*} + V_{ub}V_{cb}^{*} &= 0 \qquad (uc) \label{eq:CKMRelnUC} \end{equation} \end{subequations}
Here I've divided the relations first into those between rows and then between columns, using the amsmath package to do the subequation labelling, alignment around the equals sign and so on. Here's the output:
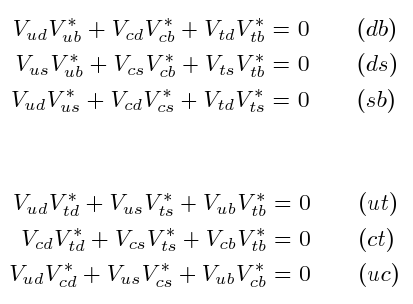
Now I don't know about you, but the unequal (math mode) spacing of the flavour indices, the variations in subscript height between conjugated and unconjugated V's and the different widths of the terms look pretty scrappy to me. Let's try to fix these little visual quirks.
Improved method
Now a more careful approach, using the maybemath, amsmath and hepnicenames packages. This time, we need to put a bunch of definitions in the preamble or in a personal style/package/class:
\usepackage{amsmath,maybemath,hepnicenames} \DeclareRobustCommand{\mymath}[1]{\ensuremath{\maybebmsf{#1}}} \DeclareRobustCommand{\CkmElementConj}[2]{\mymath{V_{{#1}{#2}}^{*}}\xspace} \DeclareRobustCommand{\CkmElement}[2]{\mymath{V_{{#1}{#2}}^{\phantom{*}}}\xspace} \DeclareRobustCommand{\Vud}{\CkmElement{\Pup}{\Pdown}} \DeclareRobustCommand{\Vus}{\CkmElement{\Pup}{\Pstrange}} \DeclareRobustCommand{\Vub}{\CkmElement{\Pup}{\Pbottom}} \DeclareRobustCommand{\Vcd}{\CkmElement{\Pcharm}{\Pdown}} \DeclareRobustCommand{\Vcs}{\CkmElement{\Pcharm}{\Pstrange}} \DeclareRobustCommand{\Vcb}{\CkmElement{\Pcharm}{\Pbottom}} \DeclareRobustCommand{\Vtd}{\CkmElement{\Ptop}{\Pdown}} \DeclareRobustCommand{\Vts}{\CkmElement{\Ptop}{\Pstrange}} \DeclareRobustCommand{\Vtb}{\CkmElement{\Ptop}{\Pbottom}} \DeclareRobustCommand{\VudConj}{\CkmElementConj{\Pup}{\Pdown}} \DeclareRobustCommand{\VusConj}{\CkmElementConj{\Pup}{\Pstrange}} \DeclareRobustCommand{\VubConj}{\CkmElementConj{\Pup}{\Pbottom}} \DeclareRobustCommand{\VcdConj}{\CkmElementConj{\Pcharm}{\Pdown}} \DeclareRobustCommand{\VcsConj}{\CkmElementConj{\Pcharm}{\Pstrange}} \DeclareRobustCommand{\VcbConj}{\CkmElementConj{\Pcharm}{\Pbottom}} \DeclareRobustCommand{\VtdConj}{\CkmElementConj{\Ptop}{\Pdown}} \DeclareRobustCommand{\VtsConj}{\CkmElementConj{\Ptop}{\Pstrange}} \DeclareRobustCommand{\VtbConj}{\CkmElementConj{\Ptop}{\Pbottom}} %% CKM element pairing for unitarity relations \newlength{\CKMPairWidth} \settowidth{\CKMPairWidth}{\Vtd\VtbConj} \DeclareRobustCommand{\@Vbox}[1]{\makebox[\CKMPairWidth]{#1}} \DeclareRobustCommand{\VCkmPair}[2]{\ensuremath{\@Vbox{{#1}{#2}}}}
These definitions are mostly for compactness. The definitions of the CKM
elements and conjugates include a superscript phantom asterisk to make the two
take up the same vertical space, and the \VCkmPair macro fixes each term to be
the same width. The flavour indices are implemented using the quark macros from
my hepnicenames package (in the hepnames set) to do the particle symbols via
commands like \Pcharm.
Now the equations themselves are written as follows,
\begin{subequations} \label{eq:CKMUnitarityRelations} \begin{align} \VCkmPair{\Vud}{\VubConj} + \VCkmPair{\Vcd}{\VcbConj} + \VCkmPair{\Vtd}{\VtbConj} &= 0 \qquad (\Pdown\Pbottom) \label{eq:CKMRelnDB} \\ \VCkmPair{\Vus}{\VubConj} + \VCkmPair{\Vcs}{\VcbConj} + \VCkmPair{\Vts}{\VtbConj} &= 0 \qquad (\Pdown\Pstrange) \label{eq:CKMRelnDS} \\ \VCkmPair{\Vud}{\VusConj} + \VCkmPair{\Vcd}{\VcsConj} + \VCkmPair{\Vtd}{\VtsConj} &= 0 \qquad (\Pstrange\Pbottom) \label{eq:CKMRelnSB} \end{align} % \begin{align} \VCkmPair{\Vud}{\VtdConj} + \VCkmPair{\Vus}{\VtsConj} + \VCkmPair{\Vub}{\VtbConj} &= 0 \qquad (\Pup\Ptop) \label{eq:CKMRelnUT} \\ \VCkmPair{\Vcd}{\VtdConj} + \VCkmPair{\Vcs}{\VtsConj} + \VCkmPair{\Vcb}{\VtbConj} &= 0 \qquad (\Pcharm\Ptop) \label{eq:CKMRelnCT} \\ \VCkmPair{\Vud}{\VcdConj} + \VCkmPair{\Vus}{\VcsConj} + \VCkmPair{\Vub}{\VcbConj} &= 0 \qquad (\Pup\Pcharm) \label{eq:CKMRelnUC} \end{align} \end{subequations}
Here's the output:
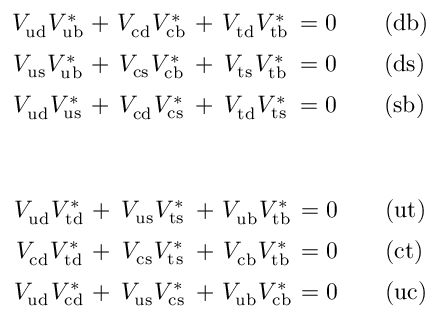
Not bad, eh? And that, as they say, is that.
Postscript: you may now find that the subdepth package makes a lot of this redundant by automatically fixing the subscript depth. That package was written long after these instructions, and since I don't need to typeset CKM relations anymore I've not tried it out. It is used by the new version of hepparticles, though, and works very nicely indeed.